Dipolar systems

2D dipolar crystals and melting

The outstanding feature of cold atomic and molecular quantum gases is the high control and tunability of microscopic system parameters via external fields. Prominent examples are the realization of low-dimensional trapping geometries, and the tuning of the contact interaction via Feshbach resonances. In a recent work [1] this control has been extended to the shape and the strength of interactions with the goal to generate new classes of potentials. In combination with low-dimensional trapping, these provide a framework for realizing new many body quantum phases and phase transitions. Specifically, these ideas have been investigated in the context of polar molecules in the strong interaction limit, where the stability of the dipolar gas is guaranteed by a confinement of the particles into a twodimensional (2D) setup. Applying appropriately chosen static and/or microwave fields allow one to design effective potentials between pairs of molecules. In turn, these potentials give rise to interesting new many-body phenomena. As an illustration, the appearance of a crystalline phase has been considered, and an associated quantum melting to a superfluid phase, for a 2D dipolar interaction.

[1] H.P. Büchler, E. Demler, M. Lukin, A. Micheli, N. Prokof'ev, G. Pupillo, P. Zoller, Strongly correlated 2D quantum phases with cold polar molecules: controlling the shape of the interaction potential, cond-mat/0607294

Circuit cavity QED and molecular quantum memory

During the last few years we have witnessed a remarkable development in the control of coherent quantum systems both on the quantum optical as well as the solid state side. Further, new technologies for the fabrication and miniaturisation of on-chip traps for atomic and molecular (AMO) systems have been invented, which provide the basis for the - still outstanding - task to create a coherent interface between AOM and solid state based qubits.

We have investigated a hybrid quantum circuit where ensembles of cold polar molecules serve as long-lived quantum memories and optical interfaces for solid state quantum processors. The large dipole moments of polar molecules and their rotational level splitting of a few GHz provide the necessary conditions to achieve strong coupling to the quantized field of a high-Q microwave cavity, which itself is part of a solid state quantum processor. For this setup we have discussed basic quantum information protocols, including a swap from the cavity photon bus to the molecular quantum memory, and a deterministic two qubit gate between different ensembles. Detailed investigations of collision-induced dephasing of ensemble qubits show that an ensemble of polar molecules does indeed serve as long lived quantum memory for superconducting quantum circuits. The proposal for a molecular ensemble quantum memory [1] and related work on the coupling of a single molecule to a microwave cavity [2] have been submitted for publication. This work has been performed in collaboration with D. DeMille (Yale), R. Schoelkopf (Yale), M. Lukin (Harvard) and J. Doyle (Harvard).

[1] P. Rabl, D. DeMille, J. M. Doyle, M. D. Lukin, R. J. Schoelkopf, P. Zoller, Hybrid Quantum Processors: molecular ensembles as quantum memory for solid state circuits, quant-ph/0604140

[2] A. Andre, D. DeMille, J. M. Doyle, M. D. Lukin, S. E. Maxwell, P. Rabl, R. J. Schoelkopf, P. Zoller, Polar molecules near superconducting resonators: a coherent, all-electrical, molecule-mesoscopic interface, quant-ph/0605201

Lattice spin models

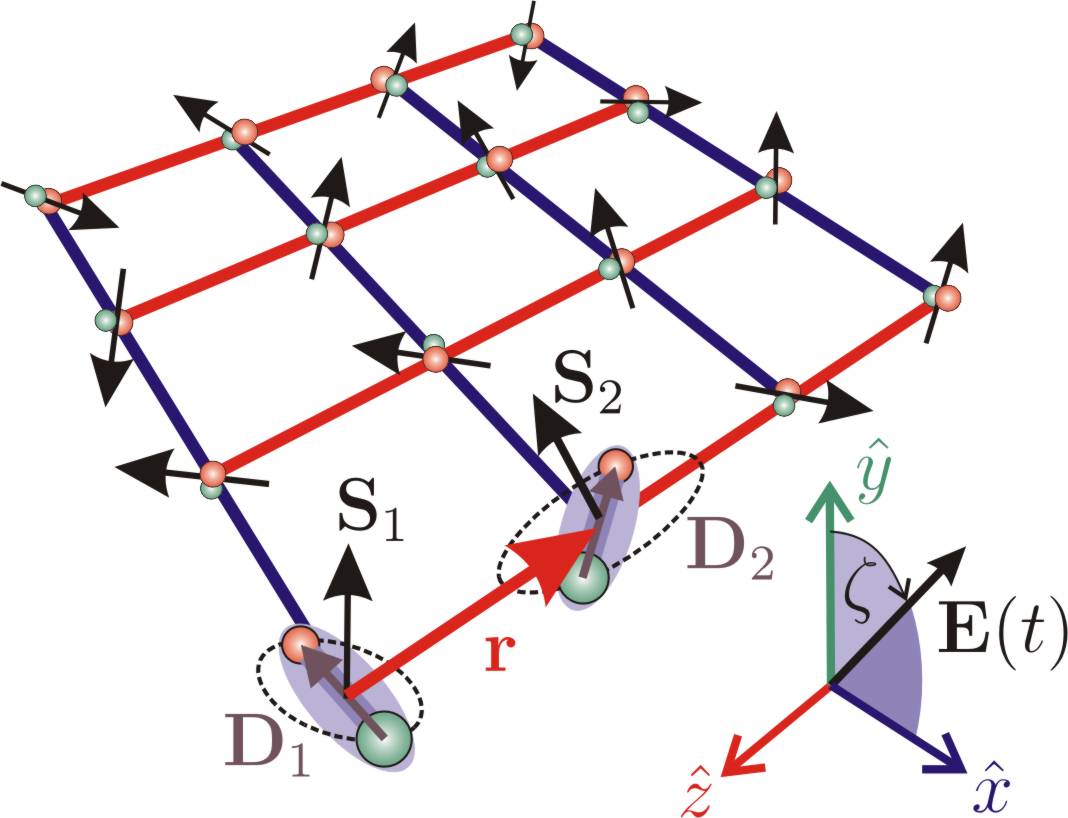
There is growing interest in states of matter with topological order. These are characterized by highly stable ground states robust to perturbations that preserve the topology, and which support excitations with so-called anyonic statistics. Topologically ordered states can arise in two-dimensional lattice-spin models, which were proposed as the basis for a new class of quantum computation. Part of the recent research of our group investigated how the relevant hamiltonians for such spin lattice models can be systematically engineered with polar molecules stored in optical lattices. Here, the spin is represented by a single-valence electron of a heteronuclear molecule. The combination of microwave excitation with dipole–dipole interactions and spin–rotation couplings enables building a complete toolbox for effective two-spin interactions with designable range, spatial anisotropy and coupling strengths.

[1] A. Micheli, G. K. Brennen, P. Zoller, A toolbox for lattice spin models with polar molecules, Nature Physics 2, 341 (2006)