Welcome to the wiki page of

Project Coral
Exponential quadrature

coordinated by Marlis Hochbruck (Karlsruhe).

The group members are:

• Ghasem Abbasi (Tehran)
• Gábor Csörgő (Budapest)
• Hicham El Boujaoui (Marrakesh)
• Hatice Tavli (Chemniz)

The project description can be downloaded from here.

Discussion of Project Coral.

 

The aim of this project is to study the numerical approximation to solutions of linear abstract differential equations

u'(t) + Au(t) = f(t),u(t0 + ) = u0

on a Banach space X by exponential quadrature formulas.

To define such quadrature formulas we choose non-confluent collocation nodes c_,...,c_s and define approximations 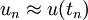, where t_n = t₀ + n_h, n = 0,1,... via

with weights

Here, l_j is the Lagrange interpolation polynomial

The project involves

• construction of exponential quadrature formulas
• convergence analysis in different Banach spaces (e.g. in L^p) and with different boundary conditions
• numerical experiments (using Matlab or any other programming language)

References

1. M. Hochbruck, A. Ostermann: Exponential Runge-Kutta methods for parabolic problems, Appl. Numer.
2. Math., vol. 53, no. 2-4, pp. 323-339 (2005)